크루스칼 알고리즘 (Kruskal's Algorithm)

Minimum Spanning Tree 문제를 해결하기 위해서 보통 두 가지 종류의 알고리즘 중 하나를 선택하여 사용한다.

 

1. 프림 알고리즘 (Prim's Algorithm)
2. 크루스칼 알고리즘 (Kruskal's Algorithm)

 

이 두 가지 알고리즘 모두 MST 문제에서 최적의 값을 도출할 수 있음이 이미 증명되어 있다.

 

이번에는 크루스칼 알고리즘에 대하여 알아보도록 하겠다.

 

크루스칼 알고리즘은 모든 Edge들에 대해 Weight가 작은 것부터 큰 순으로 Sorting 해놓고 Weight가 작은 Edge부터 MST에 포함시켜 나가는 방식을 사용하는데, 여기에서  핵심은 Edge를 추가했을 때 사이클 생성 여부를 체크하여 사이클이 생성되지 않는 경우 해당 Edge를 MST에 추가한다는 것이다.

 

모든 Edge를 확인했는데 V-1개의 Edge가 선택되지 않은 경우가 있다면 그래프가 Disconnected 되어있다는 뜻이다.

 

 

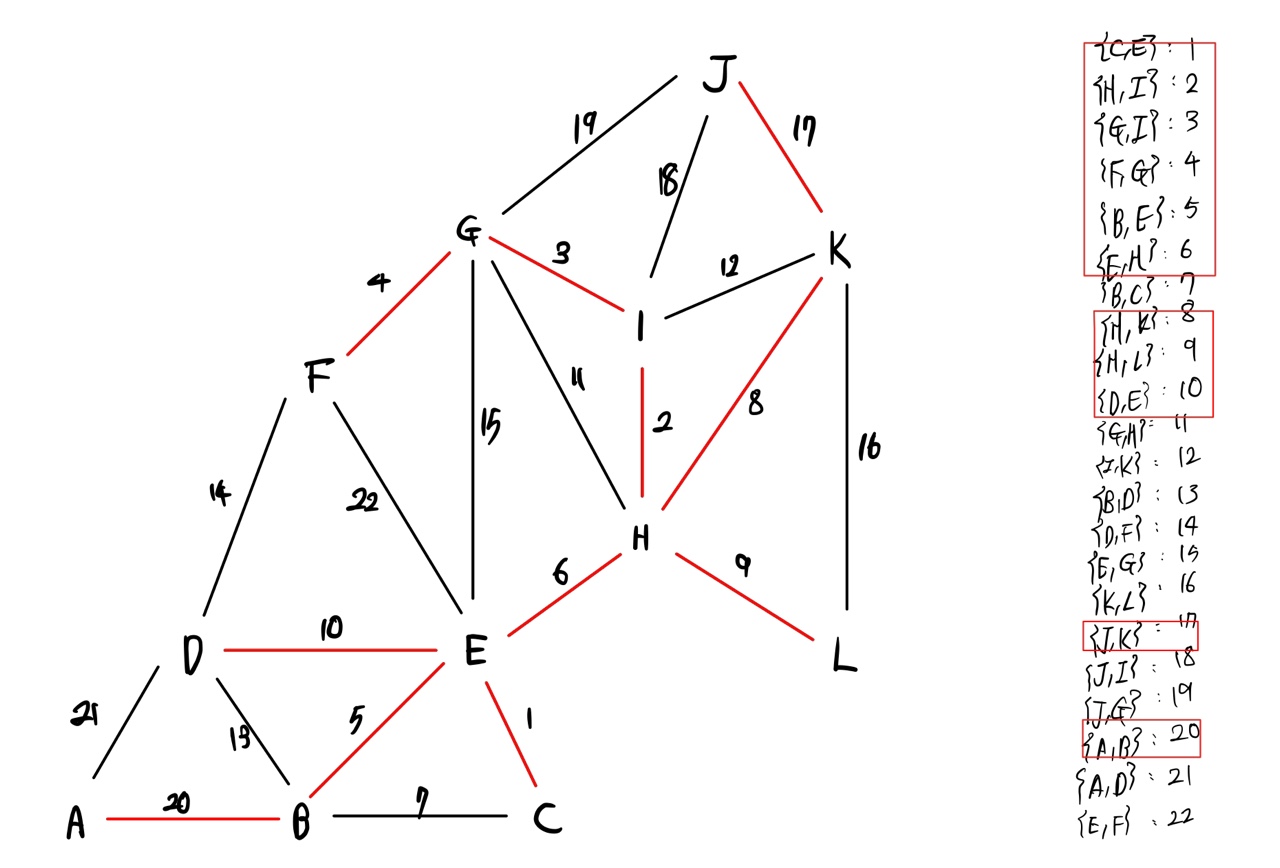
주어진 그래프에서 모든 Edge들에 대해 가중치가 낮은 것부터 높은 것까지 차례로 나열해두고 사이클을 생성하지 않는 Edge에 대해서 MST에 추가한다.

 

크루스칼 알고리즘의 시간 복잡도에 대해 알아보도록 하자.

 

- Edge Sorting : O(ElogE)

- Edge 추가할 때마다 사이클이 생기는지 매번 체크해야 한다.

  - E : Edge의 개수, V : 사이클 체크하는 비용 : O(|E|log(|E|)+ |E|*|V|)

- Edge의 최대 : V²이므로 logE = logV (시간 복잡도는 계수를 생략하므로)

 

*해당 게시글은 K-Mooc 허재필 교수님의 강의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고>의 강의 내용을 참고하여 작성되었음을 알립니다.